Tensor Basics
Perform standard imports
import torch
import numpy as np
torch.__version__
'1.12.0+cu113'
Converting NumPy arrays to PyTorch tensors
A torch.Tensor is a multi-dimensional matrix containing elements of a single data type.
Calculations between tensors can only happen if the tensors share the same dtype.
In some cases tensors are used as a replacement for NumPy to use the power of GPUs .
arr = np.array([1,2,3,4,5])
print(arr)
print(arr.dtype)
print(type(arr))
[1 2 3 4 5]
int64
<class 'numpy.ndarray'>
x = torch.from_numpy(arr)
# Equivalent to x = torch.as_tensor(arr)
print(x)
tensor([1, 2, 3, 4, 5])
# Print the type of data held by the tensor
print(x.dtype)
torch.int64
# Print the tensor object type
print(type(x))
<class 'torch.Tensor'>
np.arange(0.,12.)
array([ 0., 1., 2., 3., 4., 5., 6., 7., 8., 9., 10., 11.])
arr2 = np.arange(0.,12.).reshape(4,3)
print(arr2)
[[ 0. 1. 2.]
[ 3. 4. 5.]
[ 6. 7. 8.]
[ 9. 10. 11.]]
x2 = torch.from_numpy(arr2)
print(x2)
print(x2.type())
tensor([[ 0., 1., 2.],
[ 3., 4., 5.],
[ 6., 7., 8.],
[ 9., 10., 11.]], dtype=torch.float64)
torch.DoubleTensor
Here torch.DoubleTensor refers to 64-bit floating point data.
Tensor Datatypes
| TYPE | NAME | EQUIVALENT | TENSOR TYPE |
|---|---|---|---|
| 32-bit integer (signed) | torch.int32 | torch.int | IntTensor |
| 64-bit integer (signed) | torch.int64 | torch.long | LongTensor |
| 16-bit integer (signed) | torch.int16 | torch.short | ShortTensor |
| 32-bit floating point | torch.float32 | torch.float | FloatTensor |
| 64-bit floating point | torch.float64 | torch.double | DoubleTensor |
| 16-bit floating point | torch.float16 | torch.half | HalfTensor |
| 8-bit integer (signed) | torch.int8 | CharTensor | |
| 8-bit integer (unsigned) | torch.uint8 | ByteTensor |
Copying vs. sharing
torch.from_numpy()
torch.as_tensor()
torch.tensor()
There are a number of different functions available for creating tensors. When using torch.from_numpy() and torch.as_tensor(), the PyTorch tensor and the source NumPy array share the same memory. This means that changes to one affect the other. However, the torch.tensor() function always makes a copy.
# Using torch.from_numpy()
arr = np.arange(0,5)
t = torch.from_numpy(arr)
print(t)
tensor([0, 1, 2, 3, 4])
arr[2]=77
print(t)
tensor([ 0, 1, 77, 3, 4])
# Using torch.tensor()
arr = np.arange(0,5)
t = torch.tensor(arr)
print(t)
tensor([0, 1, 2, 3, 4])
arr[2]=77
print(t)
tensor([0, 1, 2, 3, 4])
Creating tensors from scratch
Uninitialized tensors with .empty()
torch.empty() returns an uninitialized tensor. Essentially a block of memory is allocated according to the size of the tensor, and any values already sitting in the block are returned. This is similar to the behavior of numpy.empty().
x = torch.empty(4, 3)
print(x)
tensor([[1.0994e-35, 0.0000e+00, 3.3631e-44],
[0.0000e+00, nan, 0.0000e+00],
[1.1578e+27, 1.1362e+30, 7.1547e+22],
[4.5828e+30, 1.2121e+04, 7.1846e+22]])
Initialized tensors with .zeros() and .ones()
torch.zeros(size)
torch.ones(size)
It’s a good idea to pass in the intended dtype.
x = torch.zeros(4, 3, dtype=torch.int64)
print(x)
tensor([[0, 0, 0],
[0, 0, 0],
[0, 0, 0],
[0, 0, 0]])
x = torch.ones(4, 4)
print(x)
tensor([[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]])
Tensors from ranges
torch.arange(start,end,step)
torch.linspace(start,end,steps)
Note that with .arange(), end is exclusive, while with linspace(), end is inclusive.
x = torch.arange(0,18,2).reshape(3,3)
print(x)
tensor([[ 0, 2, 4],
[ 6, 8, 10],
[12, 14, 16]])
x = torch.linspace(0,18,12).reshape(3,4)
print(x)
tensor([[ 0.0000, 1.6364, 3.2727, 4.9091],
[ 6.5455, 8.1818, 9.8182, 11.4545],
[13.0909, 14.7273, 16.3636, 18.0000]])
Tensors from data
torch.tensor() will choose the dtype based on incoming data:
x = torch.tensor([1, 2, 3, 4])
print(x)
print(x.dtype)
#changing datatypes
x.type(torch.int32)
tensor([1, 2, 3, 4])
torch.int64
tensor([1, 2, 3, 4], dtype=torch.int32)
You can also pass the dtype in as an argument. For a list of dtypes visit https://pytorch.org/docs/stable/tensor_attributes.html#torch.torch.dtype
x = torch.tensor([8,9,-3], dtype=torch.int)
print(x)
print(x.dtype)
tensor([ 8, 9, -3], dtype=torch.int32)
torch.int32
Random number tensors
torch.rand(size) returns random samples from a uniform distribution over [0, 1)
torch.randn(size) returns samples from the “standard normal” distribution [σ = 1]
Unlike rand which is uniform, values closer to zero are more likely to appear.
torch.randint(low,high,size) returns random integers from low (inclusive) to high (exclusive)
x = torch.rand(4, 3)
print(x)
tensor([[0.6030, 0.2285, 0.8038],
[0.1230, 0.7200, 0.3957],
[0.7680, 0.6049, 0.2517],
[0.2586, 0.7425, 0.6952]])
x = torch.randn(4, 3)
print(x)
tensor([[ 0.2165, -0.0686, 0.2015],
[ 0.7441, 0.7225, 1.4614],
[-2.3071, 0.4702, 0.6524],
[-0.4017, -0.5270, 1.1353]])
x = torch.randint(0, 5, (4, 3))
print(x)
tensor([[3, 2, 0],
[2, 3, 2],
[3, 4, 3],
[0, 2, 0]])
Random number tensors that follow the input size
torch.rand_like(input)
torch.randn_like(input)
torch.randint_like(input,low,high)
these return random number tensors with the same size as input
x = torch.zeros(2,5)
print(x)
tensor([[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.]])
x2 = torch.randn_like(x)
print(x2)
tensor([[-0.4551, 0.0819, 2.0344, -0.7828, -0.0693],
[-1.0297, -0.0456, -0.8849, 2.3125, 0.4777]])
The same syntax can be used with
torch.zeros_like(input)
torch.ones_like(input)
x3 = torch.ones_like(x2)
print(x3)
tensor([[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.]])
Setting the random seed
torch.manual_seed(int) is used to obtain reproducible results
torch.manual_seed(42)
x = torch.rand(2, 3)
print(x)
tensor([[0.8823, 0.9150, 0.3829],
[0.9593, 0.3904, 0.6009]])
torch.manual_seed(42)
x = torch.rand(2, 3)
print(x)
tensor([[0.8823, 0.9150, 0.3829],
[0.9593, 0.3904, 0.6009]])
Tensor Operations
Perform standard imports
import torch
import numpy as np
Indexing and slicing
Extracting specific values from a tensor works just the same as with NumPy arrays
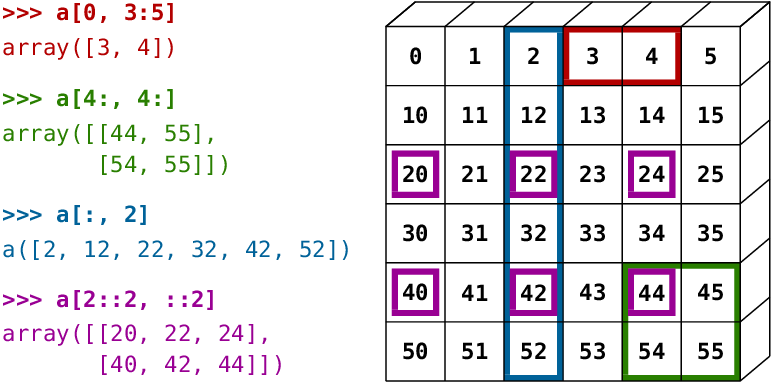
Image source: http://www.scipy-lectures.org/_images/numpy_indexing.png
x = torch.arange(6).reshape(3,2)
print(x)
tensor([[0, 1],
[2, 3],
[4, 5]])
# Grabbing the right hand column values
x[:,1]
tensor([1, 3, 5])
# Grabbing the right hand column as a (3,1) slice
x[:,1:]
tensor([[1],
[3],
[5]])
Reshape tensors with .view()
view() and reshape() do essentially the same thing by returning a reshaped tensor without changing the original tensor in place.
There’s a good discussion of the differences here.
x = torch.arange(10)
print(x)
tensor([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
x.view(2,5)
tensor([[0, 1, 2, 3, 4],
[5, 6, 7, 8, 9]])
x.view(5,2)
tensor([[0, 1],
[2, 3],
[4, 5],
[6, 7],
[8, 9]])
# x is unchanged
x
tensor([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
x = x.reshape(5,2)
x
tensor([[0, 1],
[2, 3],
[4, 5],
[6, 7],
[8, 9]])
Views reflect the most current data
z = x.view(2,5)
x[0]=234
print(z)
tensor([[234, 234, 2, 3, 4],
[ 5, 6, 7, 8, 9]])
Views can infer the correct size
By passing in -1 PyTorch will infer the correct value from the given tensor
x.view(2,-1)
tensor([[234, 234, 2, 3, 4],
[ 5, 6, 7, 8, 9]])
x.view(-1,5)
tensor([[234, 234, 2, 3, 4],
[ 5, 6, 7, 8, 9]])
Tensor Arithmetic
Adding tensors can be performed a few different ways depending on the desired result.
As a simple expression:
a = torch.tensor([1,2,3], dtype=torch.float)
b = torch.tensor([4,5,6], dtype=torch.float)
print(a + b)
tensor([5., 7., 9.])
As arguments passed into a torch operation:
print(torch.add(a, b))
tensor([5., 7., 9.])
With an output tensor passed in as an argument:
result = torch.empty(3)
torch.add(a, b, out=result) # equivalent to result=torch.add(a,b)
print(result)
tensor([5., 7., 9.])
Changing a tensor in-place
a.add_(b) # equivalent to a=torch.add(a,b)
print(a)
tensor([5., 7., 9.])
In the above example: a.add_(b) changed a.
Basic Tensor Operations
| OPERATION | FUNCTION | DESCRIPTION |
|---|---|---|
| a + b | a.add(b) | element wise addition |
| a - b | a.sub(b) | subtraction |
| a * b | a.mul(b) | multiplication |
| a / b | a.div(b) | division |
| a % b | a.fmod(b) | modulo (remainder after division) |
| ab | a.pow(b) | power |
| OPERATION | FUNCTION | DESCRIPTION |
|---|---|---|
| |a| | torch.abs(a) | absolute value |
| 1/a | torch.reciprocal(a) | reciprocal |
| $\sqrt{a}$ | torch.sqrt(a) | square root |
| log(a) | torch.log(a) | natural log |
| ea | torch.exp(a) | exponential |
| 12.34 ==> 12. | torch.trunc(a) | truncated integer |
| 12.34 ==> 0.34 | torch.frac(a) | fractional component |
| OPERATION | FUNCTION | DESCRIPTION |
|---|---|---|
| sin(a) | torch.sin(a) | sine |
| cos(a) | torch.sin(a) | cosine |
| tan(a) | torch.sin(a) | tangent |
| arcsin(a) | torch.asin(a) | arc sine |
| arccos(a) | torch.acos(a) | arc cosine |
| arctan(a) | torch.atan(a) | arc tangent |
| sinh(a) | torch.sinh(a) | hyperbolic sine |
| cosh(a) | torch.cosh(a) | hyperbolic cosine |
| tanh(a) | torch.tanh(a) | hyperbolic tangent |
| OPERATION | FUNCTION | DESCRIPTION |
|---|---|---|
| $\sum a$ | torch.sum(a) | sum |
| $\bar a$ | torch.mean(a) | mean |
| amax | torch.max(a) | maximum |
| amin | torch.min(a) | minimum |
| torch.max(a,b) returns a tensor of size a containing the element wise max between a and b | ||
For example, torch.div(a,b) performs floor division (truncates the decimal) for integer types, and classic division for floats.
Use the space below to experiment with different operations
a = torch.tensor([1,2,3], dtype=torch.float)
b = torch.tensor([4,5,6], dtype=torch.float)
print(torch.add(a,b).sum())
tensor(21.)
torch.min(a) + b.max()
tensor(7.)
Dot products
A dot product is the sum of the products of the corresponding entries of two 1D tensors. If the tensors are both vectors, the dot product is given as:
$\begin{bmatrix} a & b & c \end{bmatrix} \;\cdot\; \begin{bmatrix} d & e & f \end{bmatrix} = ad + be + cf$
If the tensors include a column vector, then the dot product is the sum of the result of the multiplied matrices. For example:
$\begin{bmatrix} a & b & c \end{bmatrix} \;\cdot\; \begin{bmatrix} d \ e \ f \end{bmatrix} = ad + be + cf$
Dot products can be expressed as torch.dot(a,b) or a.dot(b) or b.dot(a)
a = torch.tensor([1,2,3], dtype=torch.float)
b = torch.tensor([4,5,6], dtype=torch.float)
print(a.mul(b)) # for reference
print()
print(a.dot(b))
tensor([ 4., 10., 18.])
tensor(32.)
Matrix multiplication
2D Matrix multiplication is possible when the number of columns in tensor A matches the number of rows in tensor B. In this case, the product of tensor A with size $(x,y)$ and tensor B with size $(y,z)$ results in a tensor of size $(x,z)$
</div>
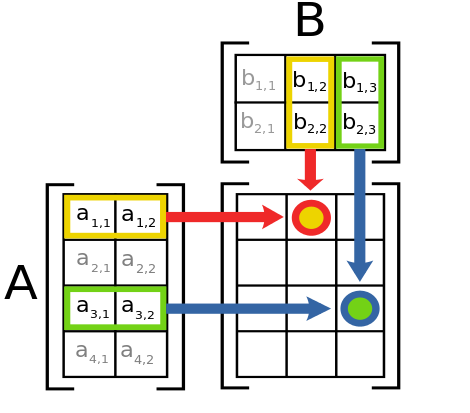
Matrix multiplication can be computed using torch.mm(a,b) or a.mm(b) or a @ b
a = torch.tensor([[0,2,4],[1,3,5]], dtype=torch.float)
b = torch.tensor([[6,7],[8,9],[10,11]], dtype=torch.float)
print('a: ',a.size())
print('b: ',b.size())
print('a x b: ',torch.mm(a,b).size())
a: torch.Size([2, 3])
b: torch.Size([3, 2])
a x b: torch.Size([2, 2])
print(torch.mm(a,b))
tensor([[56., 62.],
[80., 89.]])
print(a.mm(b))
tensor([[56., 62.],
[80., 89.]])
print(a @ b)
tensor([[56., 62.],
[80., 89.]])
Matrix multiplication with broadcasting
Matrix multiplication that involves broadcasting can be computed using torch.matmul(a,b) or a.matmul(b) or a @ b
t1 = torch.randn(2, 3, 4)
t2 = torch.randn(4, 5)
print(torch.matmul(t1, t2).size())
torch.Size([2, 3, 5])
t1 = torch.randn(2, 3)
t1
tensor([[ 0.7596, 0.7343, -0.6708],
[ 2.7421, 0.5568, -0.8123]])
t2 = torch.randn(3).reshape(3,1)
t2
tensor([[ 1.1964],
[ 0.8613],
[-1.3682]])
print(torch.mm(t1, t2))
tensor([[2.4590],
[4.8718]])
Advanced operations
L2 or Euclidian Norm
See torch.norm()
The Euclidian Norm gives the vector norm of $x$ where $x=(x_1,x_2,…,x_n)$.
It is calculated as
${\displaystyle \left|{\boldsymbol {x}}\right|{2}:={\sqrt {x{1}^{2}+\cdots +x_{n}^{2}}}}$
When applied to a matrix, torch.norm() returns the Frobenius norm by default.
x = torch.tensor([2.,5.,8.,14.])
x.norm()
tensor(17.)
Number of elements
See torch.numel()
Returns the number of elements in a tensor.
x = torch.ones(3,7)
x.numel()
21
This can be useful in certain calculations like Mean Squared Error:
def mse(t1, t2):
diff = t1 - t2
return torch.sum(diff * diff) / diff.numel()
References
- Some part of this notebook are from Jose Marcial Portilla works.